USACO 2022 赛季试题解析系列(12月晋级赛-银级)

距离USACO 2022赛季第二场竞赛越来越近了，不知道大家做好准备了了吗？为方便同学了解题目思路，USACO教学组准备了《USACO题解》专题，本期进入第二期，提供2022赛季第一次竞赛中的银升金解题思路，希望能为同学们提供有用的帮助。

铜级题解回顾请点击：USACO 2022 赛季试题解析系列(12月晋级赛-铜级)

Silver Problem1

Closest Cow Wins

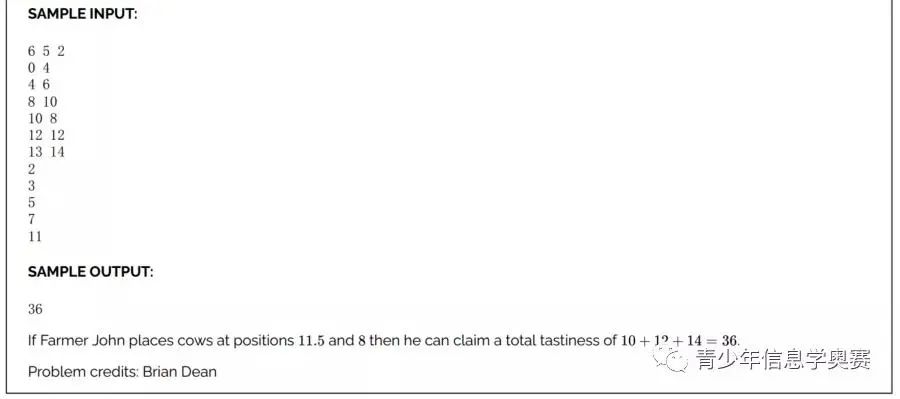
通过分析题目我们能够发现，我们能够按照Nhoj牛所在的位置把数轴分成一个个区间，每个区间内投入我们的牛，而投入牛的个数只有0头，1头和2头三种情况，因为每个区间至多投入2头牛就能控制区间内的所有草堆，所有m头牛至多可划分成m+1个区间，这样我们就把题目转化为：要统计出每个区间投放1头牛所控制的最大值 value 和 所有值all总共投放n头牛所获得的最大收益。

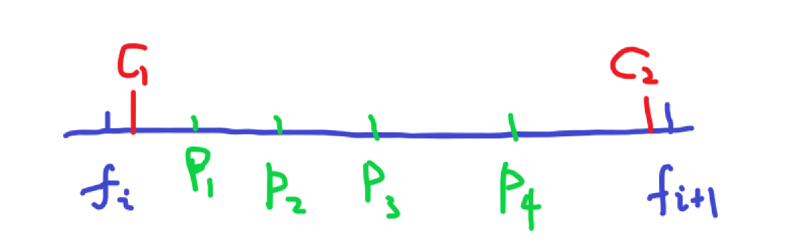
每个区间我们可以以草堆为控制点，配合双指针可以在O(n)时间内完成。

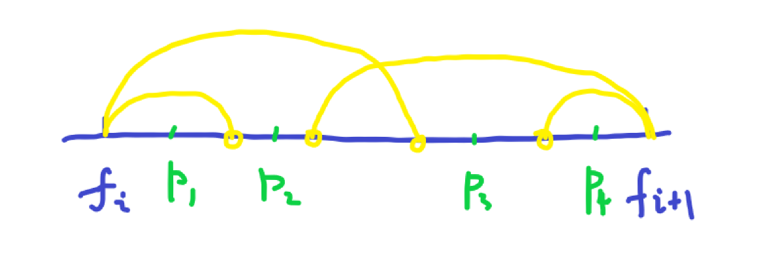
这样我们就可以用贪心来解决问题了。开一个优先队列，这个优先队列是以只放1头牛所获得收益所构成的大顶堆，这样我们每次弹出操作时，都是选择最划算的区间，也就是手里这头牛所能获得的最大价值，当一个区间被弹出时，如果是第一次被弹出，我们就把value改成all - value再放回去，表示已经放过一头牛，这样如果再放一头牛整个区间的总价值是不变的，就可以一直贪心下去了。

代码如下：

#include <bits/stdc++.h>

#define ll long long

using namespace std;

const ll MAXN = 2e5 + 5;

struct Grass

{

ll p, t;

ll l, r;

bool operator<(const Grass &a) const

{

return p < a.p;

}

} g[MAXN];

 

struct Node

{

ll value, all, cnt;

 

bool operator<(const Node &a) const {

return value < a.value;

}

};

ll k, m, n;

ll f[MAXN];

ll p[MAXN << 2], pc;

priority_queue<Node> q;

void solve()

{

ll all = 0;

ll pi = 1;

 

while (pi <= k && g[pi].p < f[1])

{

all += g[pi].t;

pi++;

}

q.push({all, all, 0});

for (int i = 2; i <= m; ++i)

{

 

all = pc = 0;

ll left = f[i - 1], right = f[i];

ll from = pi;

while (pi <= k && g[pi].p < right)

{

ll ra = min(g[pi].p - left, right - g[pi].p);

g[pi].l = g[pi].p - ra;

g[pi].r = g[pi].p + ra;

if (g[pi].l != left)

{

p[pc++] = g[pi].l;

}

if (g[pi].r != right)

{

p[pc++] = g[pi].r;

}

all += g[pi].t;

pi++;

}

if (from == pi)

{

 

continue;

}

 

p[pc++] = right;

sort(p, p + pc);

ll tt = 0;

 

ll tl = from, tr = from - 1, w = 0;

for (int j = 0; j < pc; ++j)

{

ll pos = p[j];

while (tr + 1 < pi && pos > g[tr + 1].l)

{

tr++;

w += g[tr].t;

}

while (tl < pi && pos > g[tl].r)

{

w -= g[tl].t;

tl++;

}

tt = max(tt, w);

}

q.push({tt, all, 0});

}

 

all = 0;

while (pi <= k)

{

all += g[pi].t;

pi++;

}

q.push({all, all, 0});

}

 

int main() {

cin >> k >> m >> n;

for (int i = 1; i <= k; ++i)

{

cin >> g[i].p >> g[i].t;

}

for (int i = 1; i <= m; ++i)

{

cin >> f[i];

}

sort(g + 1, g + k + 1);

sort(f + 1, f + m + 1);

solve();

ll ans = 0;

while(n>0 && !q.empty())

{

Node t = q.top();

q.pop();

ans+=t.value;

if(t.cnt==0 && t.value!=t.all){

t.cnt++;

t.value = t.all-t.value;

q.push(t);

}

n--;

}

cout << ans;

return 0;

 

Silver Problem2

Connecting Two Barns

题意为一个n个点m条边的无向图，点的编号为1到n，可以在任意点i与点j之间连边，代价为（i-j）2，现在可以最多连2条边，使得1与n连通，求最小代价。

我们可以分以下情况讨论：

1. 点1 与点n本来就连通，代价为0

2. 在点1 和点n所在连通区域选择差值最小的两个点连接1条边

3. 经过一个中转连通区域连接2条边

首先可以求出初始与 1,n 在同一连通分量的点的集合，记为 F 与 G。对于一个点 uu，在 F,G 中分别二分查找得到与其差值最小的点并尝试更新最小值。

代码如下：

#include <iostream>

#include <map>

#include <vector>

using namespace std;

int n, m;

int u[100010];

int find(int x)

{

if (x == u[x])

return x;

u[x] = find(u[x]);

return u[x];

}

int main()

{

int T;

cin >> T;

for (int t = 1; t <= T; t++)

{

map<int, vector<long long> > cb;

map<int, long long> d1, d2;

cin >> n >> m;

for (int i = 1; i <= n; i++)

u[i] = i;

for (int i = 1; i <= m; i++)

{

int x, y;

cin >> x >> y;

x = find(x);

y = find(y);

u[x] = y;

}

for (int i = 1; i <= n; i++)

{

cb[find(i)].push_back(i);

}

int from = find(1), to = find(n);

if (from == to)

{

cout << 0 << endl;

continue;

}

long long ans = 1e18;

vector<long long> &cbf = cb[from];

vector<long long> &cbt = cb[to];

for (auto p : cb)

{

long long tf = 1e18, tt = 1e18;

for (long long x : p.second)

{

int r = lower_bound(cbf.begin(), cbf.end(), x) - cbf.begin();

if (r < cbf.size())

tf = min(tf, (cbf[r] - x) * (cbf[r] - x));

if (r > 0)

tf = min(tf, (cbf[r -1 ] - x) * (cbf[r - 1] - x));

 

r = lower_bound(cbt.begin(), cbt.end(), x) - cbt.begin();

if (r < cbt.size())

tt = min(tt, (cbt[r] - x) * (cbt[r] - x));

if (r > 0)

tt = min(tt, (cbt[r -1 ] - x) * (cbt[r - 1] - x));

}

if (tf + tt < ans)

ans = tf + tt;

}

cout << ans << endl;

}

return 0;

 

Silver Problem3

Convoluted Interval

思路：这道题相对简单，用差分思想考虑，所有 ai+aj 的地方+1，所以 bi+bj+1 的地方减1。然而这是 O(n2)，但我们发现 a,b 的值域很小，所以我们可以用数组存起来，然后按值域遍历即可，就变成 O(m2)。

代码如下：

#include <iostream>

using namespace std;

int n, m;

long long cx[5010], cy[5010];

long long d[10010];

int main()

{

cin >> n >> m;

for (int i = 1; i <= n; i++)

{

int x, y;

cin >> x >> y;

cx[x]++;

cy[y]++;

}

 

for (int i = 0; i <= m; i++)

{

for (int j = 0; j <= m; j++)

{

d[i + j] += cx[i] * cx[j];

d[i + j + 1] -= cy[i] * cy[j];

}

}

for (int i = 1; i <= m * 2; i++)

d[i] += d[i - 1];

for (int i = 0; i <= m * 2; i++)

cout << d[i] << endl;

return 0;

}

本期 USACO 2022赛季12月月赛银升金题解就到这里了，我们下周金升铂金题解见，敬请期待！