Hello~昨天的题已经给大家发过预告啦~那我们先直接来看题吧!

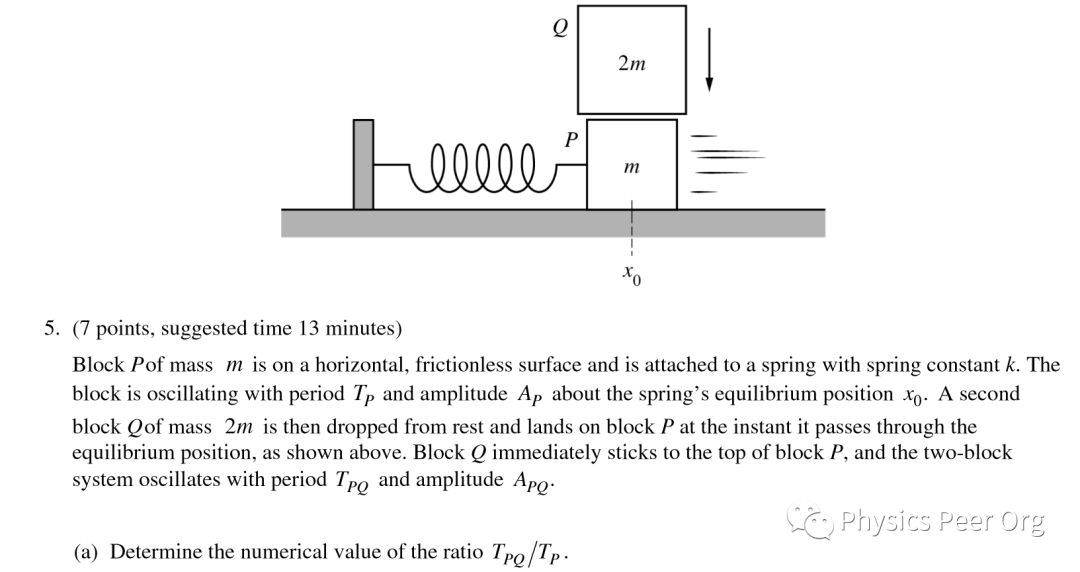
由于是波的运动,我们先判断本题主要涉及到的知识点就是简谐运动(Simple harmonic motion——SHM)
我们先回想一下SHM都有哪些特征
1.equilibrium position平衡位置,可以理解为SHM的起点位置。
2.restoring force 恢复力,是使得绳子上的质点恢复到平衡位置的力。
涉及公式: F=-kx(k是spring constant,x是displacement,负号表示相反的方向)
3. displacement 位移,在本题中绳子上的指点的位移方向是上下来回运动的,且maximum displacement 等于amplitude(振幅)。
由上面第二点我们知道restoring force始终和displacement是相反的,并且始终指向equilibrium position。
a问题意:
(a)点P和点Q在绳子上被标注出来了。
ⅰ.下图中展示了这个绳子在某一时刻,点P在最大位移处,点Q的位移为零(相较于平衡位置)请在点P和点Q处画一个箭头表明其即使速度的方向。如果速度为零,请在点的附近写v=0。
解析:
首先P点是在振幅位置处,此时这里的位移最大,但是速度最小(等于0)。
那么究竟怎么判断速度的大小及方向呢?
solution1:
首先在这一问中P在下一时刻就会向上加速运动,并且在运动到P之前是向下减速后运动到P的,所以P点就处在这两个状态的交界处,相当于是质点P先慢慢向下减速到0然后向上加速运动,所以点P的速度为0。
solution2
如果将这个绳子的displacement versus time 图像画出来,发现在最高点斜率为0,而在x-t图像中斜率代表的是速度的大小和方向,所以因此速度为0。
点Q 的速度就更好判断了,因为下一秒Q会向上运动,所以Q点的速度是向上的。
a问答案:
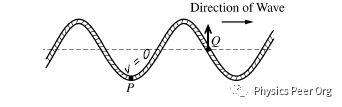
ⅱ.下图与上问为同一时刻。在P和Q点画一个表示加速度的箭头。如果加速度为零。则在旁边写上a=0即可。
1.在P点时,displacement最大,所以restoring force 最大,restoring force始终指向平衡位置(平衡位置在点P的上方),并且加速度的方向与合力的方向是一致的,所以加速度也向上。
2.在点Q时,位移x=0,所以F=0,所以a=F/m=0。
答案:
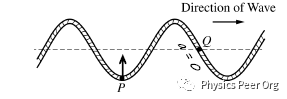
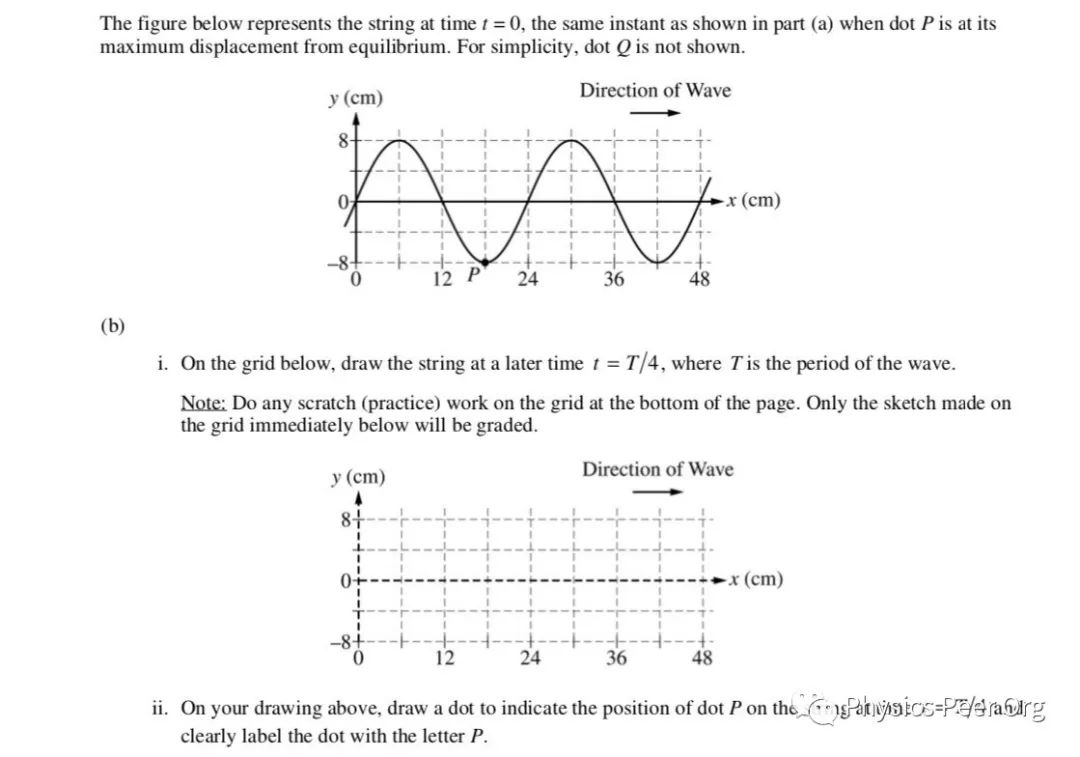
题意:
下图代表了这个绳子在t=0时,与(a)问的时间相同,点P在最大位移处,点Q的位移为零。点Q没有展现出来。
(b)
ⅰ.在下面的坐标方格中,画出在过了t=T/4(T是这个波的周期)后的图。
ⅱ.在上图画出在过了t=T/4后点P的位置。
我们都知道简谐运动的图像是正弦函数,所以用在学习三角函数中的方法先判断出周期的大小是四个格子,那么四分之一个周期的大小就是一个格子。我们想要画出在经过T/4后的图像,首先就要将原图整体向右平移一格,然后再补全图像。
同理,如果想知道在T/4之前的图像,就将图像整体向左平移一格,然后将y轴左半部分删除(因为t不能小于0)。
然后点P横坐标是不变的,因为在简谐运动中是各个质点上下运动来传递形成的波,所以质点是不会做水平位移的。
答案:
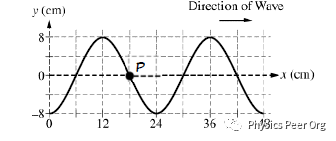
最后一问:

题意: 在经过一整个周期后,P点经过的距离是多少?(从t=0到t=T)
我们从上图可以发现,crest到平衡位置需要四分之一个周期,也就是说一个周期内质点会从crest到平衡位置4次,也就相当于4个振幅。
根据图中观察可得,振幅A=8cm 那么X=4A=32cm。