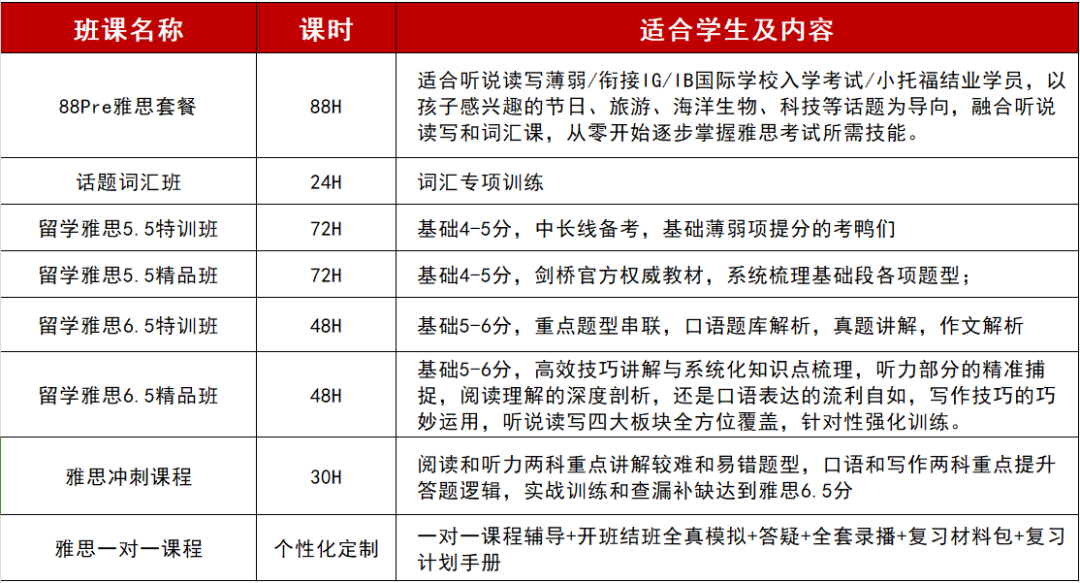
又到9月开学季,距离11月的AMC10数学竞赛开赛只剩2个月的时间!时间越紧,备考方法就显得尤为重要!但是不管后续如何规划,第一步还是需要明确自己的数学基础,知道自己“几斤几两”才能更好地查漏补缺,针对性提升。
小编整理了几题AMC10真题中易错的几道题,不少同学又双叒叕不小心踩坑了,来看看你的“抵抗力”如何?

01、你“拿捏”AMC10了吗?
- AMC10 真题 示例-
01、有多少种方法可以将整数1到14分成7对,以便每对中较大的数至少是较小数的2倍?
A.108
C.126
E.144
B.120
D.132
答案:E
02、设Tk序列为坐标平面中的变形,它表明使一个平面首先围绕原点逆时针旋转平面k度,然后以 y 轴为对称轴翻转。变换序列为T1、T2、T3……Tn 。那么请问将点(1,0)返回自身的最小正整数 n 是多少?
A.359
C.719
E.721
B.360
D.720
答案:A
03、设Ln表示数1、2、3、... n 的最小公倍数,且设h为唯一正整数,使得
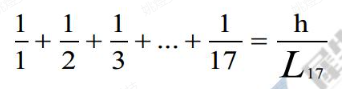
那么 h 除以17的余数是多少?
A.359
C.719
E.721
B.360
D.720
答案:C
04、通过将边为1的四个正六边形连接到边为1的正方形来形成碗。相邻六边形的边缘重合,如图所示。通过连接位于碗边缘的四个六边形顶部八个顶点获得的八边形的面积是多少?
A.6
C.5+2√2
E.9
B7
D.8
答案:B
05、假设编号为1、2、3、.…13的13张卡片排成一行。现在有个任务是以数字递增的顺序拾取它们,从左到右重复工作。在下面的示例中,卡1、2、3在第一遍中被拾取,4和5在第二遍中被拾起,6在第三遍中被捡起,7、8、9、10在第四遍中被拾起,11、12、13在第五遍中被拾起。
请问有多少种排列顺序是可以让这13张卡片在两次拾起中就能捡完的?
A.4082
C.4096
E.8191
B.4095
D.8178
答案:D
06、假设有这么一串数字,由数字0、1、2、3、4形成且它的位数是5。若j代表数字里的每个数字,j∈(1、2, 3、4),并且该串数字至少包含小于 j 的 j 位数字,那么这样的数字组合有多少种?(例如,02214满足此条件,因为它至少包含小于1的1位数字,至少包含小于2的2位数字,最少包含小于3的3位数字,以及至少包含小于4的4位数字字符串23404不满足条件,因为其不包含至少2位小于2的数字。)
A.500
C.1089
E.1296
B.625
D.1199
答案:E
07、设R 、S和T是在坐标平面中的格点(即坐标均为整数的点)处具有顶点的正方形,以及它们的内部的正方形也是如此。每个正方形的底边位于 x 轴上。R的左边缘和S的右边缘在y轴上,R包含9/4个与S相同的格点。T的顶部两个顶点在RUS中,T包含RUS中的1/4个格点。见图(未按比例绘制)。S 中位于S∩T中的点阵点的分数是R中位于RT中点阵点分数的27倍。R的边长加上S的边长再加上T的边长的最小可能值是多少?
A.336
C.338
E.340
B.337
D.339
答案:B
- AMC10竞赛备考-
01明确重难点、高频考点
代数 Algebra:代数计算技巧(因式分解、换元、展开等)ニ次函数与方程绝对值和取整函数数列和求和问题直线与圆
几何 Geometry:几何变换圆的几何性质
数论 Number theory:同余(剩余系、整除法则、同余方程)整数方程位值原理与进制
02“揪出”易错点
代数 Algebra:
应用题(审题、计数单位、建模等)
绝对值函数求解
指数、对数函数的计算
几何 Geometry:
全等/相似三角形(寻找相等角)
图形的切割增补(转化特殊三角形、特殊图形)
平面几何想象能力(文字到图像)
计数 Counting:
排列与组合的区别
避免重复计数
迭代
数论 Number theory:
质因数分解
尾数
同余
概率 Probability:
离散概率
几何概率
03注意答题节奏
1.答题节奏不是能够一蹴而就的,需要大家通过一年年的真题积累、模拟,每做完一套,就习惯性地对知识点进行一次总结。
2.AMC10竞赛需要在75分钟内解25题,相当于平均3分钟做一道题,考试的节奏非常快,类似于ACT的答题模式。
3.所以,一定要有考场的时间分配策略:
①前20道简单的题目用50分钟的时间答完,并且保证错误率能控制在1题以内。
②留25分钟出来给后面难度较高的题目。而最后这5题也就决定了学生是否能进入前5%甚至是前1%,也是很多同学力争突破瓶颈的地方。