你可能不知道贪心算法,但你一定知道活在当下。如果你知道,那么恭喜你,你已经掌握贪心算法的核心本质了!
贪心算法的理念就是不问过去,不计将来,只考虑当下。捡了芝麻丢了西瓜?不存在的!当下有西瓜,绝不碰芝麻~
贪心算法讲究的是每遇到一个子问题, 都取当下情况的最优解, 直到所有子问题被解决。
那么,贪心算法到底是怎么帮我们解决问题的呢?
我购买了一张戛纳电影节的一日票。双程机票、翻倍的酒店价格都让我的钱包越来越扁... 心痛 .jpg... 为了能最大限度薅到资本主义的羊毛,我当然会爆发出爱因斯坦的智商,来精准计算怎样的观影顺序能让我在有限的时间里看到最多的电影!传奇天主教总统传记《肯尼迪传》,小李子《花月杀手》,北野武的《首》还有缠绕三角恋《燃东》-- 统统到我碗里来!!
假设:当天有 n 部电影,第 i 部电影在 a 时开始、b 时结束。每部电影我都可以选择看或不看。但如果我选择看某部电影,那即使遇到烂片也必须全程看完。并且我不能同时观看 2 部及 2 部以上电影。
求:我最多能看几部电影?
很显然,这道题的子问题就是:从某个时刻起,应该如何选择下一场电影?
我可以有以下选择:
1、当天每次都选开始时间最早的电影;
2、当天每次都选结束时间最早的电影;
3、当天每次都选用时最短的电影;
4、当天每次都选与最少可选工作有重叠的电影。
根据以下图示,很容易证明选择 1,3,4 是不可行的!

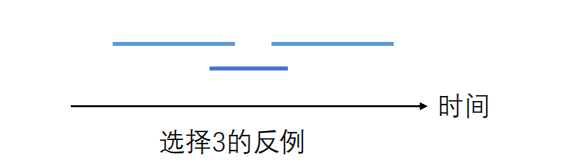
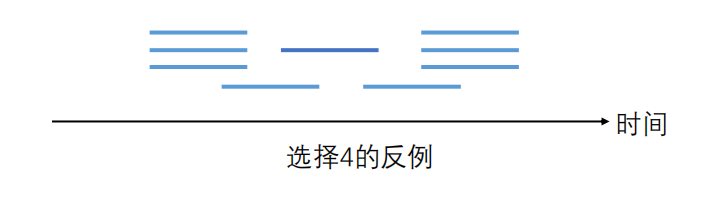
由此可见,子问题的最优解就是:每次都选结束时间最早的电影!
这就是此题的贪心策略,可选电影中结束时间最早的那场电影就是本题的局部最优解。
由于每场电影包含一个开始时间和一个结束时间,所以我们可以定义一种结构体,命名为 Movie。
Movie 中包含了开始时间和结束时间,代码如下:
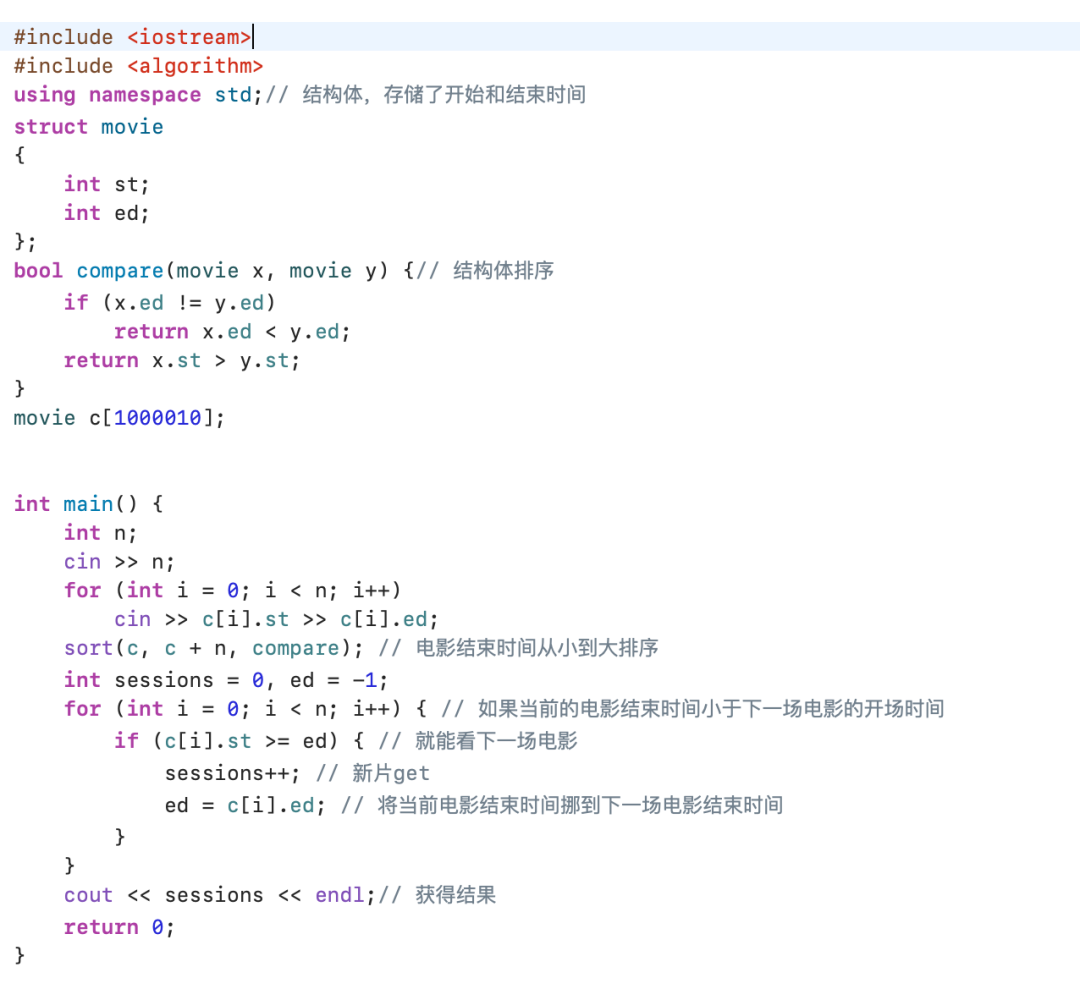
总结:
- 贪心法就是指在求解问题时,总是做出当前最好的选择(而不是整体)。
- 贪心算法没有固定的框架,算法设计的关键是贪心策略的选择。
- 贪心策略必须具备无后效性,即某个状态的选择只与当前状态有关。
小课堂
在我看来,每个人每天都在做“贪心算法”。
我们的人生都是由无数个子问题构成的,我们需要在无数个小的路口做出我们认为对的选择,但生活无法回头,即使后来我们知道我之前的选择可能并非最优解,可我们也无法从头来过。没有人可以穿越回去修改过去的选择,从而获得“全局的绝对最优解”。
因为我知道我永远只能基于当下的认知水平,在不完美的条件下做我认为最利于当下的选择,而不是在理想情况下做最优解,抱怨“为什么条件不完美”是没有意义的。不完美是人生的常态,我能做到的,只有不埋怨现状,不害怕未来,尽量不断地做出我认为对的选择。
不要将自己困囿于过去的错误中,也不要惧怕未来,抓住每一个小时做贪心算法吧!