2022年剑桥大学STEP数学考试全面解读

什么是剑桥STEP数学考试？

由剑桥大学招生考试委员会组织的STEP考试是为测试申请者数学能力而举行的笔试，其全称为Sixth Term Examination Paper，直译过来就是“第六学期考试”。

STEP成绩通常作为英国几所顶尖高等院校，包括剑桥大学、帝国理工学院、伦敦大学学院、华威大学等院校的数学、计算机等相关专业录取条件之一。尽管牛津大学数学、计算机相关专业不要求提供STEP成绩，但牛津官网上也明确建议申请者参加STEP考试。

剑桥STEP 2022考试关键日期

2022年3月1日	注册报名开放
2022年5月5日	注册报名截止
2022年6月9日	STEP 2考试日
2022年6月20日	STEP 3考试日
2022年8月18日	STEP成绩公布
2022年8月25日	STEP成绩问询截止

注：剑桥官方保留调整上述日期的权利。

特别提醒

STEP考试时间可能与A Level相关考试时间冲突，请提前做好相关考试安排。

剑桥STEP 2022考试如何报名？

考生需通过授权考试中心报名参加STEP考试：

考生所在学校是授权考试中心，则可通过学校报名和参加STEP考试。
学校不是授权考试中心，可以社会考生的身份登录British Council官网报名。
还有部分城市有校外机构，可以代社会考生报名并组织STEP考试。

报名时需提交给考试中心以下信息：

姓名、性别、出生日期及UCAS编号。
所申请大学的名称、专业及专业代码。
如因身体原因需要特殊照顾，需一并提交相关证明材料。

剑桥STEP 2022考试政策有哪些变化？

2022年剑桥STEP考试延续2021年各项政策，包括：

取消STEP 1、仅保留STEP 2和3考试。
仍采用2021版大纲，延续2019年的重要改革。
原STEP 1要求的知识点仍将在STEP 2和3中出现。
继续面向所有考生开放（没有offer的学生同样可以参加考试）。

全面解读｜剑桥STEP数学考试【2022】

注：剑桥官方保留变更STEP 2022考试政策的权利。

哪些大学和专业需要考剑桥STEP？

剑桥大学

Courses	专业名称	UCAS代码
Mathematics	数学	G100
Mathematics with Physics	数学物理	G100
Economics	经济	L100
Engineering	工程	H100

通常剑桥大学在条件录取中要求考生的STEP成绩达到等级1及以上。其中，数学专业通常要求STEP 2、3等级1、1甚至等级1、S的成绩。

自2018年起剑桥大学以下专业不再要求考STEP：

化学工程 Chemical Engineering via Engineering (H810)，但要求考ENGAA。
自然科学 Natural Sciences (BCF0)，但要求考NSAA。

自2019年起剑桥大学以下专业不再要求考STEP：

计算机 Computer Science with Mathematics (G400 BA/CS)，但要求考TMUA。

华威大学

Courses	专业名称	UCAS代码
Mathematics	数学	G100
Mathematics (Master of MATH)	数学 (四年)	G103
Mathematics and Philosophy	数学和哲学	GV15
Mathematics and Statistics	数学与统计	GG13
Mathematics and Statistics (MMathStat)	数学和统计 (四年)	GGC3
MORSE (Mathematics, Operational Research, Statistics and Economics)	数学运筹学统计与经济(四年)	G0L0
MORSE(Mathematics, Operational Research, Statistics andEconomics)	数学运筹学统计与经济	GLN0
Data Science (Mathematics, Statistics and Computer Science)	数据科学	G103

一般华威大学要求STEP成绩达到等级2及以上。尽管华威大学接受考生用MAT或TMUA代替STEP成绩，但很多考生因为各种原因错过每年10月底或11月初的MAT和TMUA考试，不得不选择参加次年6月的STEP考试。

华威大学官方给出的TMUA最低要求为6.5（满分9.0分），而MAT因为每年成绩会有所变化，无法在考试成绩统计结果出来以前给出MAT对应的最低分数。

自2018年起华威大学以下专业不再要求考STEP：

数学与商学 Mathematics and Business Studies (G1NC)
数学与经济学 Mathematics and Economics (GL11)

帝国理工

Courses	专业名称	UCAS代码
Computing	计算	G400
Computing	计算	G401
Computing (International Programme of Study）	计算 (国际项目)	G402
Computing (Management and Finance）	计算 (管理和金融)	G501
Computing (Software Engineering）	计算 (软件工程)	G600
Computing (Security and Reliability)	计算 (安全和可靠性)	G610
Computing (Artificial Intelligence and Machine Learning）	计算 (人工智能和机器学习)	G700
Computing (Visual Computing and Robotics)	计算 (视觉计算和机器人)	GG47
Mathematics and Computer Science	数学与计算机科学	GG14
Mathematics and Computer Science	数学与计算机科学	GG41

通常帝国理工计算机专业的条件录取中会带有STEP成绩要求。而数学专业则通常要求MAT，如果没有MAT成绩可以用STEP成绩替代。

一般帝国理工在条件录取中要求STEP 2或3达到等级2或1以上，或者STEP 2和3同时达到等级2甚至等级1以上。

其他大学

其他要求STEP（或MAT、TMUA）的大学包括：

伦敦大学学院（UCL）
布里斯托大学
巴斯大学
伦敦国王学院

上述大学的相关专业会在官网或录取条件中明确提出具体STEP考试和成绩等级要求。

牛津大学的数学、计算机等相关专业则要求考生必须参加自家组织的MAT数学考试（Mathematics Admissions Test）。尽管STEP成绩不作为牛津大学录取的必要条件之一，但牛津也鼓励考生参加STEP考试并提供成绩，以全面评估考生的学术能力。

剑桥STEP考试形式是怎样的？

基本信息

答题方式：线下，纸质试卷笔试

考试时长：3小时

公式表：不提供公式表，大纲中涉及的公式要求学生全部掌握，如果有超过大纲给出的公式，试题中会给出。

计算器：不允许使用计算器

词典：允许使用纸质双语词典

考试题型

自2021年起取消STEP 1考试后，STEP仅提供STEP 2和STEP 3两种考试。

题型均为计算题，不必做答所有题目，考生只需从试卷中选择6道题作答。

自2019年改革以后，STEP 2和3试卷题量由13道减少为12道，见下表：

考试	Section A	Section B	Section C	合计
STEP 2	纯数8道	力学2道	统计2道	12道
STEP 3	纯数8道	力学2道	统计2道	12道

剑桥STEP试卷样题

以下为2021年STEP 2真题：

[STEP 2, 2021Q1]

Prove, from the identities for , that

Find a similar identity for .
(i) Solve the equation

for .
(ii) Prove that if

then or .
Hence determine the solutions of equation with .

[STEP 2, 2021Q2]

In this question, the numbers , and may be complex.
(i) Let , and be real numbers. Given that there are numbers and such that

show that .
(ii) Conversely, you are given that the real numbers , and satisfy . By considering the equation , show that there exist numbers and such that the three equations hold.
(iii) Let , , and be real numbers. Given that there are distinct numbers , and such that

show, using part (i), that is a root of the equation

and write down the other two roots.
Deduce that .
(iv) Find numbers , and such that

and verify that your solution satisfies the four equations .

[STEP 2, 2021Q3]

In this question, , and are real numbers.
Let denote the largest integer that satisfies and let denote the fractional part of , so that and . For example, if , then and and if , then and .
(i) Solve the simultaneous equations

(ii) Given that , and satisfy the simultaneous equations

show that and solve the equations.
(iii) Solve the simultaneous equations

[STEP 2, 2021Q4]

(i) Sketch the curve , giving the coordinates of any stationary points.
(ii) The function is defined by for , where is the minimum possible value such that has an inverse function. What is the value of ?
Let be the inverse of . Sketch the curve .
(iii) For each of the following equations, find a real root in terms of a value of the function , or demonstrate that the equation has no real root. If the equation has two real roots, determine whether the root you have found is greater than or less than the other root.

(iv) Given that the equation has a unique positive root, find this root in terms of a value of the function .

[STEP 2, 2021Q5]

(i) Use the substitution , where is a function of , to solve the differential equation

where is a constant.
(ii) The curve with equation has the property that, for all values of except , the tangent at the point passes through the point .
(a) Given that , find for .
Sketch for . You should find the co-ordinates of any stationary points and consider the gradient of as . You may assume that as .
(b) Given that , sketch for , giving the co-ordinates of any stationary points.

[STEP 2, 2021Q6]

A plane circular road is bounded by two concentric circles with centres at point . The inner circle has radius and the outer circle has radius . The points and lie on the outer circle, as shown in the diagram, with , and .
(i) Show that I cannot cycle from to in a straight line, while remaining on the road.
(ii) I take a path from to that is an arc of a circle. This circle is tangent to the inner edge of the road, and has radius (where ) and centre .
My path is represented by the dashed arc in the above diagram.
Let .
(a) Use the cosine rule to find in terms of , and .
(b) Find also an expression for in terms of , and .
You are now given that is much less than .
(iii) Show that and are also both much less than .
(iv) My friend cycles from to along the outer edge of the road.
Let my path be shorter than my friend’s path by distance . Show that

Hence show that is approximately a fraction

of the length of my friend’s path.

[STEP 2, 2021Q7]

(i) The matrix represents an anticlockwise rotation through angle () in two dimensions, and the matrix also represents a rotation in two dimensions. Determine the possible values of and deduce that .
(ii) Let be a real matrix with , but .
Show that . Given that

show that .
Hence prove that .
(iii) Let be a real matrix.
Show that if and represents a rotation, then also represents a rotation. What are the possible angles of the rotation represented by ?

[STEP 2, 2021Q8]

(i) Show that, for ,

(ii) The sequence is defined by

Show that, for ,

(iii) Evaluate and and deduce that, for , can be written in the form

where and are integers (which you should not attempt to evaluate).
(iv) Show that for . Given that is non-zero for all , deduce that tends to as tends to infinity.

[STEP 2, 2021Q9]

Two particles, of masses and where , are attached to the ends of a light, inextensible string. A particle of mass is fixed to a point on the string. The string passes over two small, smooth pulleys at and , where is horizontal, so that the particle of mass hangs vertically below and the particle of mass hangs vertically below . The particle of mass hangs between the two pulleys with the section of the string making an acute angle of with the upward vertical and the section of the string making an acute angle of with the upward vertical. is the point on vertically above . The system is in equilibrium.
(i) Using a triangle of forces, or otherwise, show that:
(a)

(b) divides in the ratio , where

(ii) You are now given that .
Show that and determine the ratio of to in terms of the masses only.

[STEP 2, 2021Q10]

A train moves westwards on a straight horizontal track with constant acceleration , where . Axes are chosen as follows: the origin is fixed in the train; the -axis is in the direction of the track with the positive -axis pointing to the East; and the positive -axis points vertically upwards.
A smooth wire is fixed in the train. It lies in the - plane and is bent in the shape given by , where is a positive constant. A small bead is threaded onto the wire. Initially, the bead is held at the origin. It is then released.
(i) Explain why the bead cannot remain stationary relative to the train at the origin.
(ii) Show that, in the subsequent motion, the coordinates of the bead satisfy

and deduce that is constant during the motion.
(iii) Find an expression for the maximum vertical displacement, , of the bead from its initial position in terms of , and .
(iv) Find the value of for which the speed of the bead relative to the train is greatest and give this maximum speed in terms of , and .

[STEP 2, 2021Q11]

A train has seats, where . For a particular journey, all seats have been sold, and each of the passengers has been allocated a seat.
The passengers arrive one at a time and are labelled according to the order in which they arrive: arrives first and arrives last. The seat allocated to is labelled .
Passenger ignores their allocation and decides to choose a seat at random (each of the seats being equally likely). However, for each , passenger sits in if it is available or, if is not available, chooses from the available seats at random.
(i) Let be the probability that, in a train with seats, sits in . Write down the value of and find the value of .
(ii) Explain why, for ,

and deduce that, for ,

(iii) Give the value of in its simplest form and prove your result by induction.
(iv) Let be the probability that, in a train with seats, sits in . Determine for .

[STEP 2, 2021Q12]

(i) A game for two players, and , can be won by player , with probability , won by player , with probability , where , or drawn. A match consists of a series of games and is won by the first player to win a game. Show that the probability that wins the match is

(ii) A second game for two players, and , can be won by player , with probability , or won by player , with probability . A match consists of a series of games and is won by the first player to have won two more games than the other. Show that the match is won after an even number of games, and that the probability that wins the match is

(iii) A third game, for only one player, consists of a series of rounds. The player starts the game with one token, wins the game if they have four tokens at the end of a round and loses the game if they have no tokens at the end of a round. There are two versions of the game. In the cautious version, in each round where the player has any tokens, the player wins one token with probability and loses one token with probability . In the bold version, in each round where the player has any tokens, the player’s tokens are doubled in number with probability and all lost with probability .
In each of the two versions of the game, find the probability that the player wins.
Hence show that the player is more likely to win in the cautious version if and more likely to win in the bold version if .

剑桥STEP考试计分方式是怎样的？

STEP考试计分方式

考生作答6道题，每题均为20分，全卷满分120分。

尽管只需要做6道题，但不限制考生的答题数量。考生答题超过6道时，每道题都会判分，但只取得分最高的6道题计入总分。

2019年改革后STEP不再给出bonus mark，而是严格按照评分标准判分，也即每道题最高得分不超过20分。

STEP考试成绩等级

等级	含义	占比
S	Outstanding (优秀)	约前5~15%
1	Very Good (非常好)	约前15~30%
2	Good (好)	约前30~50%
3	Satisfactory (合格)	约前50~80%
U	Unclassified (不合格)	约前5~15%

历年STEP考试成绩等级划分标准

需要注意的是，尽管STEP 2、3的满分、等级都一样，但每种考试每年各个等级对应的分数阈值都不一样。

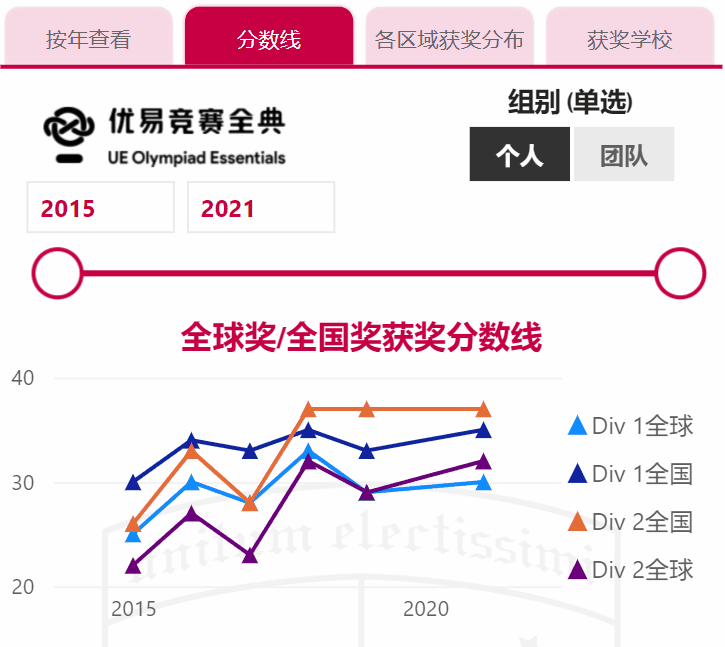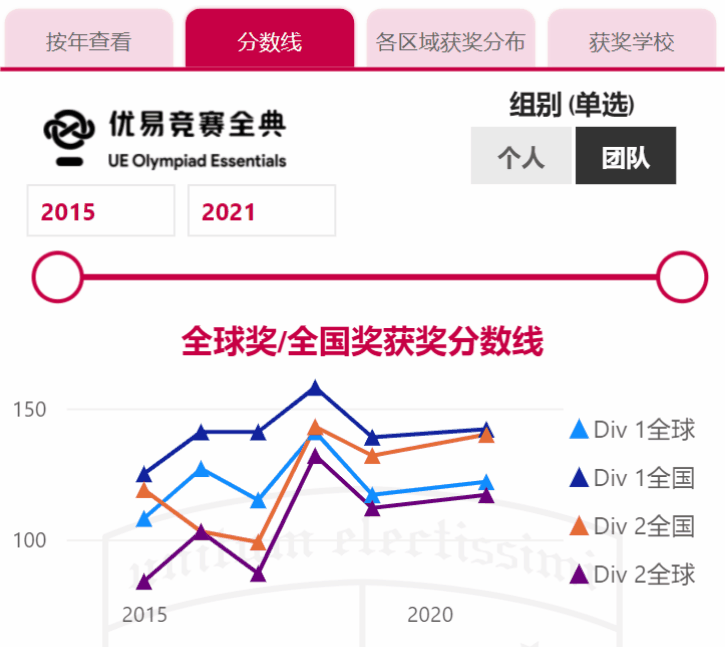
历年STEP考试成绩等级划分标准及各等级人数占比等数据可扫下方动图二维码，或点击《备考指南｜剑桥STEP数学考试》链接查看。

全面解读｜剑桥STEP数学考试【2022】

剑桥STEP考试范围是什么

考试	考试范围
STEP 1 (已取消，但仍作为STEP 2和3的知识点)	A Level数学的纯数、力学、概率统计部分，附加2021大纲要求的内容
STEP 2 (同样作为STEP 3的知识点)	AS进阶数学 (高数) 的纯数、力学、概率统计部分，附加2021大纲要求的内容
STEP 3	A level进阶数学(高数)的纯数、力学、概率统计部分，附加2021大纲要求的内容