国际数学建模挑战赛(IMMC或者IM2C),在2014年创办于美国波士顿,是一项面向全球中学生的国际性新型数学建模竞赛,其创办机构是美国数学及其应用联合会(COMAP)和香港儒莲教科文机构(NeoUnion),竞赛宗旨在于鼓励参赛者应用数学建模探索和解决现实世界的重要问题,以普及数学建模教育,增强中学生数学核心素养和科技创新能力。

2023年IMMC秋季赛已于11月21日结束,本次秋季赛高中组有2个命题任务,初中组专用1个命题任务,不同组别均可以通过自主命题参与。



今天,我们就具体来聊聊秋季赛题A的解题思路。
IMMC 2023 秋季中华赛A题
校园图书馆的智慧配送
1、背景
大学开启了智慧校园系统的建设。校园图书馆为了方便师生借阅和及时归还图书,上线了智慧图书配送模块,通过配送机器人进行图书的归还回收和借阅发放。具体做法如下:
1. 各楼宇的师生将需要归还的图书统一放在楼宇门厅的图书存放处,并报告借阅需求(见表1)。各楼宇的图书存放处只允许存放本楼宇的还书或借书;
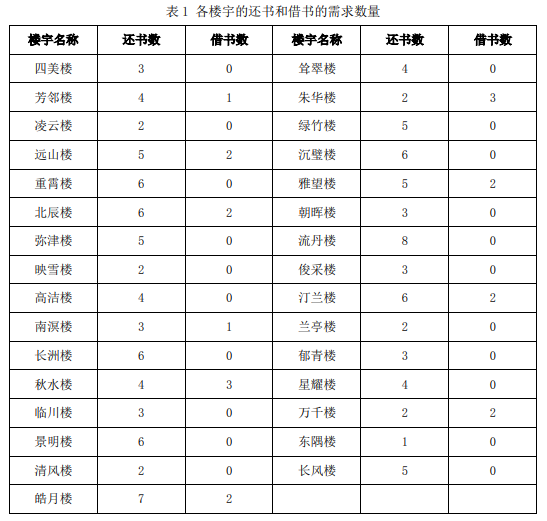
2. 现有配送机器人 A 和 B 分别从充电驻地出发(出发前均未装载书本),随后到达各处楼宇,将回收的归还图书带回图书馆,随后再次出发回收还书或发放借书;
3. 每个配送机器人单独行动,在本题目场景下不需要考虑各机器人从楼宇内取书所花的时间,也不必考虑行驶途中相遇而互换图书;
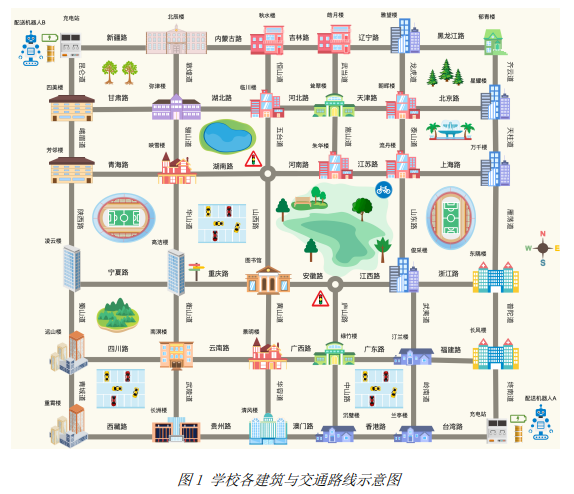
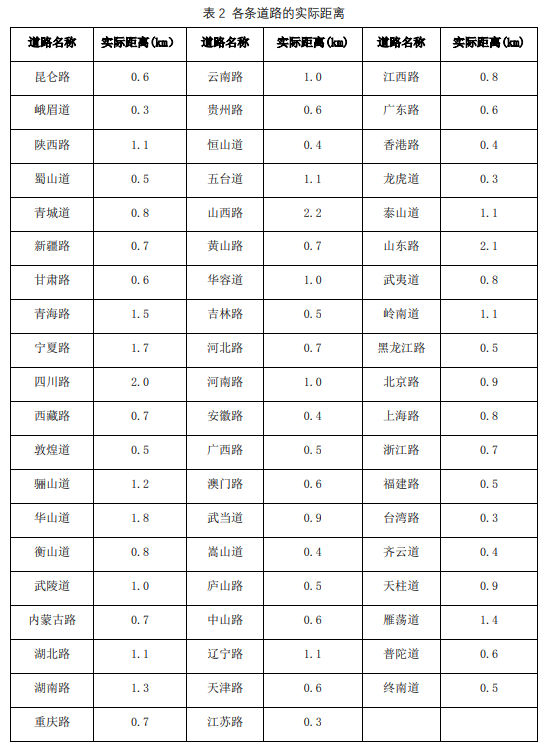
4. 在完成图书馆委派的任务后,配送机器人须返回各自初始出发的驻地进行充电。每个楼宇的位置和道路实际距离分别如图 1 和表 2 所示。每个配送机器人最多可装载 10 本书。配送机器人 A 的平均行驶速度是 8 公里/小时,配送机器人 B 的平均行驶速度是 10 公里/小时。
2、问题
1、 只考虑还书而不考虑借书的情况,配送机器人分别从充电驻地出发。请建立合适的数学模型,配送机器人以最短时间完成还书任务,并最终返回初始驻地。请说明配送机器人各自行驶的具体路线和行驶总时间。
思路点拨
这个问题的类似场景非常多,比较常见的是快递上门取件,配送机器人以最短时间完成还书任务,假设配送机器人的行驶速度变化不大,那么配送机器人走过的路径应该为最短,并最终返回初始驻地。如果机器人的装载量没有限制,那么该问题就可以简化为旅行商(TSP)问题,但事实上机器人有一定的装载量,我们便需要考虑其有限装载量。
综合考虑,这是一个单收集中心、多楼宇点、非满载的机器人完成还书任务问题,类似业务员路径规划问题(VRP)。以图书馆为坐标原点,建立坐标系,确定各楼宇的坐标和机器人的动态路径,进而建立路线分配表、射线图以及路线图。该模型比较简单直观,但不足之处在于路径选择时,当某一楼宇被其中一条路线选定后,该楼宇将不作为接下来的任意一条路线的备选收集点,每一条路线均为当前条件下的最优路线,将所有路线组合后不一定是整体的最优路径,即局部最优并非整体最优。
为此,可进一步采用顺序插入交叉算子(OIC),在遗传算法的交叉运算过程中设计的三角距离差函数作为评价标准,运用贪婪策略思想,提出的一种新的交叉算子,该算子有效的利用了局部信息,并且能很好的继承父代优秀的基因。
2、若综合考虑表 1 中还书和借书的情况,配送机器人仍从各自驻地出发,到达图书馆后可装载发放借阅的书本。行驶过程中,在发放借阅图书的同时也可以选择回收还书。请建立合适的数学模型,指导配送机器人尽快完成回收还书和发放借书任务,最终返回初始驻地,并说明配送机器人行驶的的具体路线和行驶总时间。试比较任务 1 和 2 的模型,分析不同模型的异同和各自优缺点。
思路点拨
这个问题的场景也比较多,只不过相比任务1,机器人在回收还书的之前,需要先行考虑路径的借阅情况,所以每条优化路径的还书和借书都尽可能接近装载量,综合考虑可采用多目标遗传禁忌搜索算法。在遗传算法设计中,针对收集归还书籍优化模型设计基于楼宇位置、基于不同机器人编码两种染色体;针对发放借阅书籍优化模型设计基于二进制编码的染色体,并为不同编码方式的染色体分别设计交叉、变异和修复方法,分别采用截断选择法和锦标赛选择法进行进化操作。
多目标遗传禁忌搜索算法优点是充分利用了遗传算法全局搜索能力强和禁忌搜索算法局部搜索能力强的特点;缺点是容易过早收敛,遗传过程较为复杂。此外模型未考虑时间窗的问题,对综合规划的结果有一定的影响。
参与数学建模,接受挑战
你的2023注定不同
国际数学建模挑战赛
IMMC 2023 冬季赛报名中

IMMC
重要日程
国际数学建模挑战赛( IMMC 2023)中华赛区日程安排如下:
报名/注册
2022年11月21日至2023年1月13日(冬季赛)
中华区域赛
2023年1月13日晚8时至1月17日晚8时(冬季赛)
国际赛
2023年3月8日晚8时至3月13日晚8时
答辩决赛
2023年4月下旬,香港(或择日远程在线)
颁奖典礼
IM2C中华峰会暨夏季工作坊及国际颁奖典礼:2023年暑期,地点待定(或远程在线)
IMMC
参赛规则
IMMC 2023中华赛区实行中英双语政策。中华赛程或国际赛程的论文与答辩可以中文或者英文完成。经国际赛程最终提交到国际评审环节的论文必须使用或翻译为英文。以下是参赛过程中需要着重注意的点:
1、参赛对象为中学生。每支参赛团队须由来自同一所学校的 2-4 名同学组成,且须有来自该校的至少 1 位教师担任指导老师。
2、参赛团队可自由选择参加其中一季或两季竞赛,以最佳成绩参加中华区年度总评选及晋级国际赛。团队可以自行选择以“命题论文”方式参赛,也可选择挑战自我,即以“自主 选题”(必须是现实世界问题)方式参赛。
3、 “命题论文”须在赛季规定日期的连续 96 小时内完成并提交,“自主选题论文” 则不限开始时间,但须在赛季截止时间前提交。命题论文与自选题论文将分开评审与评奖,两类论文中成绩进入首 20%的团队,将自动获得晋级国际赛程的机会。
4、IMMC 中华赛区的注册和报名网址是 immchallenge.org.cn(大陆)及 immchallenge.org.hk (大陆以外地区)。
5、中华赛区命题竞赛赛题及国际赛题可在竞赛开始之前登录中华区竞赛网站下载。
6、指导教师须保证所负责的团队在竞赛期终止后不得对论文再进行任何形式的修改。
7、指导教师须负责从参赛团队收取论文,并以 PDF 格式,将论文及控制表通过中华区竞赛网站上载到竞赛系统,提交由大中华区专家组评审。
IMMC
论文规则
参赛所提交的论文应包括一页摘要页,而且整个论文不可超过 21 页(计摘要页在内,不计附录及参考文献)。
1、论文摘要是你竞赛论文非常重要的部分。评审专家会对摘要给予相当大的评审权重,获奖论文常常是首先基于摘要的质量而从众多论文中脱颖而出。因此,一篇摘要应当清晰阐明你解决问题的方法,以及更要紧的——你最重要的结论是什么。简明扼要的摘要应当能够激发一位读者想进一步了解你工作细节的兴趣。而仅仅是重述竞赛问题,或只是从引言部分做剪剪贴贴,通常会被当成一篇质量薄弱的摘要。
2、论文正文必须全部由文字及必要的图表或其他文本组成,评审专家组不接受诸如电脑光碟等支持材料。
论文的每一页上端都必须包含本团队的控制号码及页码;建议在文档编辑中设定页上端页码序列,例如“IMMC20180214 号队伍 总 18 页之第 8 页”。学生姓名、指导老师姓名及学校名称不能出现在论文的任何一页。除了团队控制号码,论文不能包含团队其他任何标识信息。对论文规则的任何违反都会导致取消参赛资格。
参赛团队应牢记下述论文写作指引:精炼和条理性极端重要。关键陈述应展示主要观点和结果。对命题论文,要适当地阐明或重述竞赛问题;对于自主选题论文,须在问题与背景陈述中说明是在他人所提出问题与研究基础上所作的延伸、改进或深化,或说明是自己团队的原创发现和提出的问题,且要清晰定义和阐明该问题。清晰表达全部变量、前提和假设。
对问题作出分析,说明并论证所使用模型的合理性。要包含模型的设计,讨论如何检验模型。讨论你的模型或方法的长处与不足。将大段的推导、运算或举例放到附件当中,只将其在论文正文中作概述。结果的阐述必须在正文中清晰表达。
IMMC冬季赛指导方案
项目
日程


* 具体日程以后续安排为准