为了帮助大家更清晰直接地了解AMC10晋级AIME的比例,我们在MAA网站统计了相关数据,并为大家呈现出来。俗话说,知己知彼百战不殆,只有清楚定位和差距,学习起来才更有目的性。
通过2012年至2021年秋季AMC10 A卷和B卷的DHR分数线及晋级AIME的比例(见下图),不难看出,2020年以来的三次AIME晋级率较之前有了明显的提升。
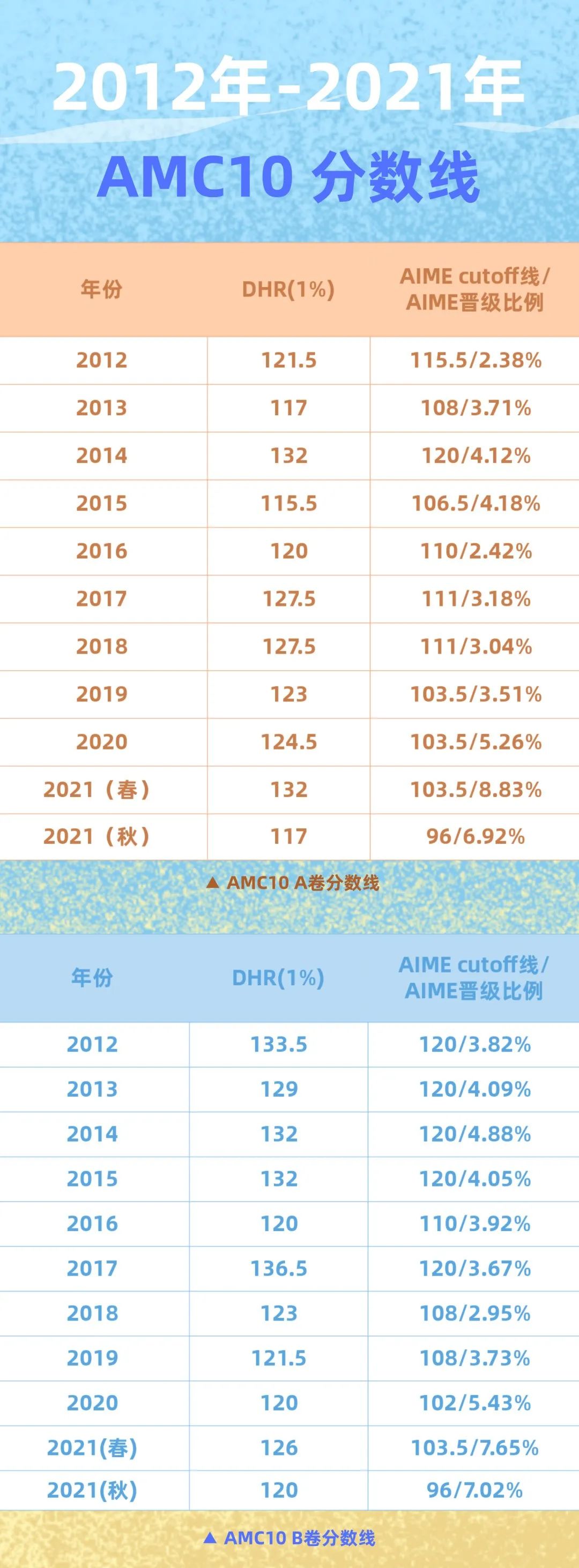
AMC10 A卷晋级AIME的比例在2019年及之前始终处于较为温和的上下波动中,2012年晋级率最低,为2.38%,2015年晋级率最高,为4.18%,差值为1.8%。但是,在2020年至2021年秋季的三场考试中,晋级率却出现了较大的上涨,分别为5.26%,8.83%(历年最高)和6.92%。
同样地,AMC10 B卷晋级AIME的比例在2019年及之前也是处于少量的动态变化中,2018年晋级率最低,为2.95%,2014年晋级率最高,为4.88%,差值为1.93%。在2020年至2021年秋季的三场考试中,AMC10 B卷晋级率则出现了较大的上涨,分别为5.43%,7.65%(历年最高)和7.02%。
AMC10 是什么?AIME又是什么?
了解完晋级比例,接下来,我们共同关注AMC10和AIME的基本信息介绍。
AMC10基本信息介绍
AMC10是美国高中数学赛事中的一项,主要针对高一年级及以下学生,该活动开始于2000年,于每年的11月中下旬举行。AMC10分A赛和B赛,难度相当,并无太大差异,且分数线分别制定,学生可任选一项参加。今年的AMC10活动已经全部结束,点击A卷和B卷关键词可以查看题目详情。
AMC10活动的目的是通过在测试中解决富于挑战性的问题,提高学生在数学方面的兴趣及问题解决能力,活动内容为除去微积分以外的高中数学, 由于考题是为从一般学校的普通学生到重点学校的优秀生中的每一位而设计的,因此测验范围由易到难,尽管考题都很具挑战性,但又在学生们力所能及的范围内。因为考察能力及知识面的范围很广,因此考生的成绩分布也很广,但通常获得120分以上的考生比例较低。
AMC10的另一个目的是发掘一些在数学方面有才华的学生,让校方能重视这些学生的存在,好的数学家就是这样被发掘、鼓励并获得发展的。在AMC10活动中,如果排名在前2.5%,肯定会受邀参加美国数学邀请赛(AIME),实际录取比例会更大一些。
当然了,学习 AMC10 可以为后续备考 AMC12 及 AIME 打下坚实基础,是拿下更高奖项的一个好帮手。
AIME基本信息介绍
AIME 全称American Invitational Mathematics Examination, 是介于AMC10、AMC12及美国数学奥林匹克竞赛(USAMO)之间的一个数学竞赛,竞赛开始于1983年,在每年的2月举行,一共两次,分为AIME I和AIME II。两次考试和AMC10/12的A卷和B卷考试模式类似,难度和效力基本相同。中国考生只能选择一场参加,一般参加AIME I 的考生居多。
AIME考题相当有难度,考生一般不能通过猜测得到正确答案.考试内容为除去微积分外的中学数学。与美国高中数学竞赛及美国数学奥林匹克竞赛一样,考题都能用不超过微积分外的中学教学方法解决。AIME的目的是确定大学之前阶段在数学方面杰出的学生,选拔美国数学奥林匹克竞赛的参加者。该考试可以为有数学方面优势的高中生提供进一步挑战并提供认识其才干的机会,而且它的实用价值在于考前的准备及考后对考题的进一步思考和讨论。
美国就读的考生如果可以在AIME活动中拿下好成绩,还有机会参加后续的USAJMO和USAMO活动,这是更具含金量的数学赛事,绝对可以拿到简历上大夸特夸。
AMC10晋级AIME的秘诀是什么?
纵观往年,AMC10如果想要晋级AIME至少要排到前5%左右才算稳妥。如何脱颖而出?当然是刷真题、熟悉并掌握考点。通过查看自己不熟悉的考点并针对性进行真题训练,考生才能有效查漏补缺,针对性提升,从而实现快速进步。
此外,我们参加AMC10一方面是熟悉AMC考试流程,提高数学兴趣,另一方面,也是为进入AIME并在AIME考试中取得高成绩做准备。所以,对于学习能力不错的考生,降维打击不失为一个好方法。通过练习AIME试题,训练技巧,考生可以为AMC10做好充分准备。不过该建议并不适用于所有考生,大家量力而行哈。如果你觉得AIME试题过于困难,还是以打好基础为首要任务。
考虑到一些人可能好奇AMC10和AIME的考察区别,老师还是为大家做一下简单的介绍。
差异一: 不同的考试形式
从75分钟25题的选择题(AMC10),变成3小时15题的填空题(AIME),巨大的考试形式的差异,这意味着我们不再可以用选择题的答题技巧(如排除法、试数法、度量法等),而是要硬碰硬地去解决每一道题目。在相对比较充足的时间内,理解题意,联系对应的知识点和技巧,通过一步一步地推理和计算,得到正确的结果。这非常考验数学的基本功,也考验心态和计算的稳定性。
差异二: 更多的知识点
AIME的大部分考点都是与AMC12一致的,此外在几何、数论、组合模块各多了少量的知识点,这些知识点大多比较复杂,一般出现在AIME的后5题中,掌握这些知识点是冲击高分的关键。但是不要忘记前10题中,多数还是AMC10和12的核心知识点,因此巩固强化AMC部分的内容也是很重要的。
差异三: 更加灵活和综合的题目
AIME题目的最大特点就是灵活性、综合性和多样性。因此需要考生有很强的思维发散性,不要禁锢于某些刻板的公式和套路,而是真正去理解、思考、联想,找到隐藏在众多表面线索背后的本质。
➤ 灵活性:AIME里很多题目的考察不注重固定的知识点(性质或公式),而是背后的一些数学思想。例如代数部分,无论是对数题、三角题、复数题,都可能会考察一些代数变形的思想和技巧,如整体代换、因式分解、递推方法、对称式和轮换式、自相似、赋予代数式几何含义等等。这些技巧都非常灵活,不是死记硬背就可以套用的公式,需要考生拿到题目时,进行思考、分析、尝试,确定最合适的方法,然后再进行求解。
➤ 综合性:AIME的很多题目都可能会涉及多个模块的知识点,即涉及交叉领域的题目。例如一道三角函数的题目,可能会牵扯复数和多项式的技巧以及几何的性质;一道几何的题目,可能会用复数和坐标系的方法;一道代数的题目如果有很多整数的条件,可能会和数论有很大的关系;一道概率计算的题目,可能最终是一个递推数列求解或者多重数列求和的问题。
➤ 多样性:AIME的题目往往会有很多的切入点,也会有多种解法。例如一道组合题目,可能可以用分类讨论加枚举解决,可能可以用递推进行计算,也可能用一一对应的方法一步解决。一道几何题,可能可以用勾股和相似解决,可能可以用三角暴力计算解决,也可能用建坐标系的方法解决。因此越“多才多艺”的同学,在做AIME题的时候,越是能够找到最合适的方法,提高自己的正确率。
其次,了解AMC10和AIME知识点差异也很重要。相较AMC10,AIME更多加入了以下知识点的考察:
➤ 代数:对数、三角函数、复数与单位根、多项式的根、圆锥曲线、三维坐标系、多重数列求和;
➤ 几何:三角形的多心问题、根轴与根心、塞瓦定理(Mass point方法)、位似变换、圆幂、圆内接四(多)边形、内心与圆外切四边形、正余弦定理、 Stewart定理;
➤ 数论:高次同余方程、指数型同余计算问题(费马小定理与欧拉定理、LTE引理、阶与原根相关定理)、线性不定方程、 中国剩余定理;
➤ 组合:无穷时间状态的期望问题、标数递推、生成函数计数、递推计数、插板法