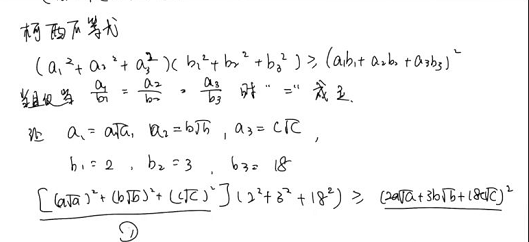在AMC的考试中,一般而言,相关考题的考察点相对固定,只要牢记对应的公式。不怕遇到这一部分的问题时没有解题思路。其中柯西不等式就是一个重要的知识点之一,今天,详细为大家介绍一下柯西不等式。
柯西不等式
柯西不等式,又称柯西-布尼亚科夫斯基-施瓦茨不等式(Cauchy–Bunyakovsky–Schwarz inequality),是柯西在研究数学分析中的“流数”问题时得到的。该不等式被认为是最重要的数学不等式之一,在线性代数、数学分析等多个领域都有着广泛的应用。
柯西不等式的特点是左边是平方和的积,简记为方和积,右边是乘积和的平方。且有着有着众多的表述形式,例如:一般形式、复数形式、积分形式等。

柯西不等式的直接应用:
例:已知x,y满足x+3y=4,求4x2+y2的最小值。
分析:方法一,大家看到该题后的直接想法可能是换元,把关于x,y的双元变量变换为关于x或y的一元变量问题,再借助于二次函数的思想可以解决。方法二,由于其结构特征与柯西不等式的形式非常相似。
这个知识点在2022年AMC Test B L1&L2 里面有应用到,考察的就是柯西不等式的应用。