现“铸剑杯”数学赛道报名者可通过赛氪竞赛官网进行注册并报名,欢迎各院校参赛者自愿报名参加。
组委会为助力大学生学习、巩固大学数学学习内容,现开放大学数学学习题库,数学爱好者可免费添加学习。同时组委会将在竞赛结束前,持续更新数学学习经验分析。请持续关注比赛!
一、设f(X)是多项式,给了几个f(X)参与计算的极限的式子,求f(X)表达式:
(1)通过观察极限的值确定f(X)的最高次项
(2)确定完最高次项之后用待定系数法
二、涉及几何的问题或工程上的实际问题,要进行建模,构造函数
就算可能写不出表达式,也建立数学关系,因为有的时候可能只需要从概念上进行评判即可,不一定需要得到具体的值(看清题目要求的或者要证明的东西与哪个知识或定理类似)
三、一个好长的式子(有规律变化)极限值等于一个常数的证明题
(1)夹逼定理(整体一起夹逼,巧用放缩)(只要是有规律的多项式,哪怕项数是有限个甚至比较少,都可以尝试夹逼定理)
(2)尝试化简式子本身,有时候可以加减相消或者裂项相消
四、求分式函数的间断点的类型:
(1)分式函数在其定义区间内一般都是连续的,所以间断点一般出现在使得分母为零的点上。要在没有约分的情况下,把所有使得分母为零的点求出来。
(2)判断是什么间断点一定要严格按照定义来
五、最大值和最小值函数:
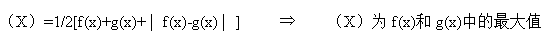
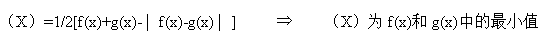
六、解函数解析式:
利用“函数表示与变量字母无关的特性”,配凑出关于f(x)的多元一次方程组,最后解方程即可
七、证明式1=式2:
利用“函数表示与变量字母无关的特性”,配凑出关于f(x)的多元一次方程组,最后解方程即可
八、等价替代需要注意的:
(1)式子中没有ln(x+1),只有lnx,那么就用lnx~(x-1)等但是使用此方法一定要注意x→什么数,满不满足等价替换的条件
(2)加减不能等效替换,一定不能。实在要用的话,就一定要先拆开,再一项项单独替换,而且一定要注意替换的过程中,每一项的极限值是否存在
九、证明数列单调:
(1)差值法Xn+1-Xn≥0
(2)比值法Xn+1/Xn≥1
十、证明数列单调已知一个条件,判断这个条件能不能推出函数可导或者已知函数可导,判断能不能推出某个条件:
一定要写导数的表达式,从定义上判断
十一、求反函数的导数:
(1)先求此函数本身的导数,反函数导数就是原函数导数的倒数
(2)等式两边同时对y求导即可(注意求反函数的导数不需要对调x和y,且最后结果的表达式要用x来表示)
十二、证明函数在区间内有界:
即证该区间内|f(x)|≤M(常数)
MATH 竞赛介绍
由国家国防科技工业局指导、中国和平利用军工技术协会主办、《中国军转民》杂志社承办的“铸剑杯”国防素养大赛自 2020年起已成功举办了3届,共吸引了上千所院校的9万余名选手参赛。
在第四届“铸剑杯”国防素养大赛国防科技单元中设立算法与逻辑思维专项赛。此专赛项与其它国防科技类赛项为同一级别赛事,为加速我国数理行业人才发展,现“铸剑杯”数学赛道报名者可通过赛氪竞赛官网进行注册并报名,欢迎各院校参赛者自愿报名参加。
MATH 报名方式
点击下方链接进行报名:https://new.saikr.com/vse/GFMATH?ces=public
MATH 主办单位
主办单位:中国和平利用军工技术协会
指导单位:国家国防科技工业局
承办单位:《中国军转民》杂志社
MATH 竞赛规则
1、试卷满分及考试时间
试卷满分为100分,考试时间为180分钟.
2、答题方式
答题方式为闭卷、笔试.
3、试卷内容结构
数学A类:数学分析80% 高等代数(矩阵理论)20%
非数学B类:高等数学80% 线性代数(矩阵理论)20%
非数学C类:微积分相关知识
1)竞赛为个人赛,依据赛题难度分为数学A类、非数学B类、非数学C类,报名时可根据个人实际情况选择组别参赛。(报名时无须选择类别,A、B、C三类均不限制参赛选手学历,本科生、研究生、高职高专生考试时可直接选择想要参加类别的考场)
2)竞赛全程线上进行,需要提交电子版作品(手写图片拍照上传即可)。
3)赛题将于竞赛开始时在竞赛考场内部公布,分为数学类和非数学类两个组别,不邮寄书面题目。
MATH 大赛奖项
本次竞赛分组别、分考场进行评奖,设立一、二、三等奖及优秀奖,获奖比例(根据实际参赛人数计算):
一等奖:5%;二等奖:15%;三等奖:30%;优秀奖:若干。
MATH 时间安排
报名时间:即日起至2024年12月27日
数学类竞赛时间:2024年12月28日9:00至12:00
非数学类竞赛时间:2024年12月29日9:00至12:00
MATH 联系方式
QQ :1451942322(陈老师)
微信:19822023476(陈老师)