SAT数学 | 一道DSAT不等式难题

今天，我们要探讨的是DSAT中一个有点难度的问题：旅游月票与单程票的成本比较。这个问题就像是你在日常生活中可能会遇到的决策问题，它不仅涉及到建立和解决不等式，还展示了数形结合在不等式问题中的重要作用。如下所示：

首先，我们需要理解月票和单程票的定价机制。月票的优势在于它提供了无限次的乘坐，而单程票则需要每次乘坐时单独购买。月票的定价策略是针对那些经常乘坐公共交通工具的人设计的，他们如果经常使用公共交通，那么月票的成本效益就会显现出来。

这个问题是关于如何确定购买月票比单独购买单程票更划算的最小单程乘坐次数数量。题目中提到，月票的价格是95美元，允许无限次数的乘坐，而单程票的价格分别是1.50美元、2.50美元和3.50美元。

●接下来，我们要确定的是，购买月票比单独购买单程票更划算的最小单程乘坐次数。为了找到这个数字，我们可以采用以下步骤：

1. 假设最贵单程票：由于我们想要找到月票成本低于单程票成本的最小点，我们应该假设每次乘坐都是最昂贵的单程票，即3.50美元。为什么呢？

月票的价格是固定的$95，而单程票的价格有三种：$1.50、$2.50 和 $3.50。为了找出月票更划算的最小单程乘坐次数，我们应该考虑单程票价格最高的情况，因为这样月票的划算门槛会更低。如下图所示

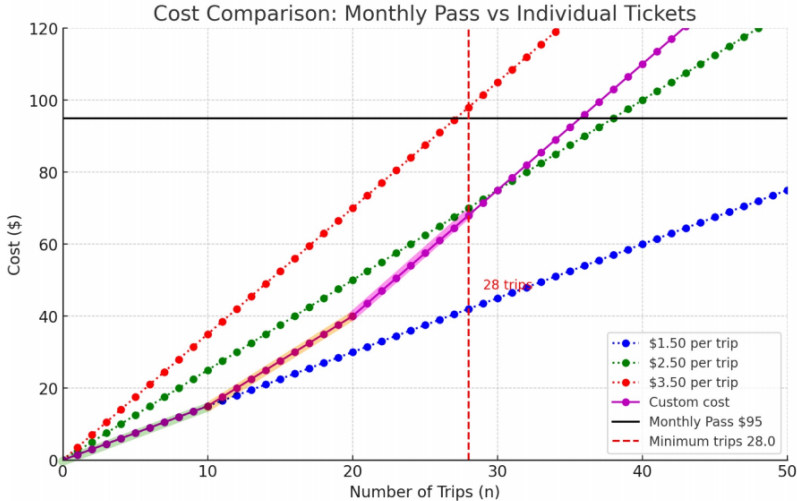
，可见，红线与cost = 95的交点最左，也就是最贵的（红色的）月票的划算门槛最小。哪怕是采取混合购买单程票的方式（如紫色折线所示），如图，紫色折线与cost = 95的交点也不如最贵（红色）月票的划算门槛小。

简而言之，选择单程票价最高值计算，是为了更快地达到月票的总成本，从而更容易地确定月票何时开始变得划算。

2. 建立不等式：我们可以建立一个不等式来表示这种情况：95美元（月票价格）小于3.50美元乘以单程乘坐次数的数量（n）。即 95 < 3.50n。

3. 解不等式：将不等式两边都除以3.50美元，我们得到27.14 < n。这意味着如果一个人一个月内乘坐的次数超过27.14次，那么购买月票的成本就会低于单独购买单程票的成本。

4. 考虑实际情况：由于单程乘坐的次数必须是整数，我们不能购买27.14张票，所以我们需要向上取整到最接近的整数，即28。

5. 结论：因此，如果一个人一个月内乘坐公共交通的次数至少是28次，那么购买月票的成本就会低于单独购买单程票的成本。

这个问题的难度被标记为“Hard”。总结来说，选择最昂贵的单程票进行计算是一种策略，从而降低计算量。借助数形结合的思想，不难发现这一点。

总结一下：

图形化解释：如果我们将不同价格的单程票看作不同的曲线，月票成本线（$95）与这些曲线的交点将告诉我们月票变得划算的点。最贵的单程票（红色曲线）与月票成本线交点最左，表示月票的划算门槛最小。

混合购买策略：即使考虑混合购买不同价格的单程票（紫色折线），其与月票成本线的交点也会比最贵的单程票的划算门槛来得晚。选择最贵的单程票价格进行计算，是为了快速确定月票何时变得划算。